The arctangent of -1 is -pi/4 (that is -45°). Why? Because the tangent of -pi/4 is -1. The arctangent function precisely seeks that angle.

• pi is “greek pi” and equals 3.14159265358979. pi is a mathematical constant representing the ratio of a circle's circumference to its diameter.
• -pi/4 equals -0.785398163397448. It represents an angle in radians and is negative one-fourth of a full π angle. Converting this value to degrees gives "-45°", meaning a 45° angle in the clockwise direction (negative) from the positive x-axis. In trigonometry, this often denotes an angle in the fourth quadrant of the Cartesian plane.
• Arctangent is the inverse function of Tangent. arctan(-1) equals -0.785398163397448 radians (-45 degrees).
• The tangent of -0.785398163397448 equals -1. In other words, -1 is the tangent of -π/4.

What does “Arcotangent” mean?

The arctangent, denoted as arctan, is a mathematical function that allows us to determine the angle from the value of its tangent.

The tangent function takes an angle and returns a number: tan(a) = x

The arctangent function performs the inverse operation: it takes a number and returns the angle whose tangent is that number: arctan(x) = a

When the tangent function is applied to an angle α expressed in radians, the result is a real number representing the ratio between the opposite leg and the adjacent leg of a right triangle with angle α.

Tactile Graphics Examples

Open the tactile graphics environment via Tools/Braille/Tactile Graphics and write:

a = -pi/4
b = arctan(-1)
MsgBox(a, b)

The two values a and b are identical and are expressed in radians. To convert a radian value to degrees, use the following instruction:

d = RadToDeg(a)
MsgBox(d)

The result is -45.

The inverse of arctan is tan. For example:

c = tan(-pi/4)
MsgBox(c)

The result is -1. This can be converted back to -pi/4 with:

b = arctan(-1)
MsgBox(b)

bTactile Code for the Arctangent Curve

Plot of the Arctangent Curve

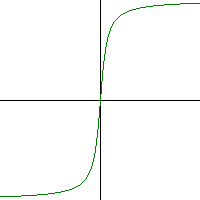
Interesting facts

The arctangent of -1, denoted as arctan(-1), is one of the most frequently asked questions in educational and practical trigonometry contexts. This value, equal to -π/4 (i.e., -45°), frequently recurs because it represents a simple, symmetric, and significant case for many applications.

It's commonly queried because it provides a straightforward, comprehensible, and memorable example. The angle -π/4 is one of the "notable values" in trigonometry, used to explain concepts like inverse functions, quadrants, symmetries, and signs of trigonometric functions.

In computer graphics, calculating the angle between two points often requires the arctangent function. For example, in video games or interactive interfaces when an arrow needs to "point" toward an on-screen target, the formula arctan(dy/dx) is frequently used – which may return exactly -1 in symmetric cases.

GPS navigation systems or mapping applications use arctangent to calculate directions between geographic coordinates. In perfectly diagonal zones, the arctangent of -1 precisely represents the -45° angle relative to the positive axis.

In engineering and physics, arctangent is used in phase calculations for complex numbers or vectors, such as when determining the direction of an electric field, force, or velocity.

Vector graphics and technical drawing also rely fundamentally on the arctan function to determine inclinations and rotations. A diagonal with a slope of -1 visually corresponds to a line inclined at -45°, commonly seen in symmetric layouts and compositions.

Finally, a special curiosity: Even in Biblos' bTactile language we've discussed – designed for creating tactile graphics to be explored by blind individuals – arctangent finds its purpose! Drawing a -π/4 angle becomes an engaging way to create a -45° slanted line, perfectly recognizable under the fingers. It blends mathematics, programming, and tactile perception into a learning experience that... leaves a mark!

For further support you can subscribe the Biblos Group on Facebook.