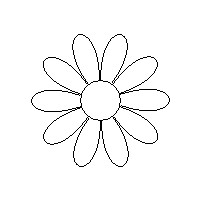
Ho commentato il codice per spiegare il ragionamento e il procedimento di Disegno. Il Linguaggio di Grafica Tattile di Biblos consente di utilizzare la Programmazione per il Disegno di figure stampabili a Rilievo. L'Insegnante che volesse avvalersi di questo strumento trova in Biblos un Ambiente con cui far apprendere al proprio Studente Matematica, geometria, Informatica... con la capacità di toccare con le dita il risultato del proprio Studio.

***

// Disegna un fiore utilizzando istruzioni vettoriali
// Biblos Tactile Graphic di Giuseppe Di Grande

// Reimposto la Dimensione dell'area Grafica
// Omettendo questa Istruzione, il fiore sarà disegnato nell'area Grafica configurata nelle impostazioni Braille
GraphicSize(200,200)

// Numero di petali del fiore
// 360 è la costante dell'angolo giro. Il valore 10 è il numero di petali
// pt è la variabile che conterrà il fattore angolare di incremento per disegnare 10 petali
pt = 360 / 10

// Ricava il centro del fiore, dividendo la larghezza e l'altezza dell'area Grafica per 2
cx = width / 2
cy = height / 2

// Ricava la Dimensione del fiore, scegliendo in base al suo punto centrale
If cx < cy
r1 = cx * 0.2
r2 = cx * 0.9
Else
r1 = cy * 0.2
r2 = cy * 0.9
EndIf

// Imposta il centro del fiore e disegna la sua corolla
GraphicOrigin(cx,cy)
Circle(cx,cy,r1+1)

// Calcola le coordinate del primo petalo
// Calcolo quattro coordinate del petalo, utili all'Istruzione del Disegno
// Mi avvalgo di alcune istruzioni trigonometriche
f = DegToRad(180)
x1 = cx + (sin(f) * r1)
y1 = cy + (cos(f) * r1)
x2 = cx + (sin(f) * r2)
y2 = cy + (cos(f) * r2)
f = DegToRad(180-pt)
x3 = cx + (sin(f) * r2)
y3 = cy + (cos(f) * r2)
x4 = cx + (sin(f) * r1)
y4 = cy + (cos(f) * r1)

// Disegna tutti i petali del fiore
// Utilizzo un ciclo for con uno step equivalente all'incremento angolare di un petalo
// La variabile g contiene i gradi dell'Orientamento del petalo
// Utilizzo l'Istruzione per il Disegno di una curva quadratica di bezier, avvalendomi del parametro di rotazione
For g = 0 to 359 step pt
Spline(x1,y1,x2,y2,x3,y3,x4,y4,g)
EndFor

***

Per ulteriore supporto ci si può iscrivere nel Gruppo di Biblos su Facebook.